TLDR: We recommend. Asymmetric certified strength The problem, which requires proven robustness for only one class and reflects real-world adversarial scenarios. This focused setting allows us to introduce feature-convex classifiers, which produce closed-form and deterministic validation radii on the order of milliseconds.
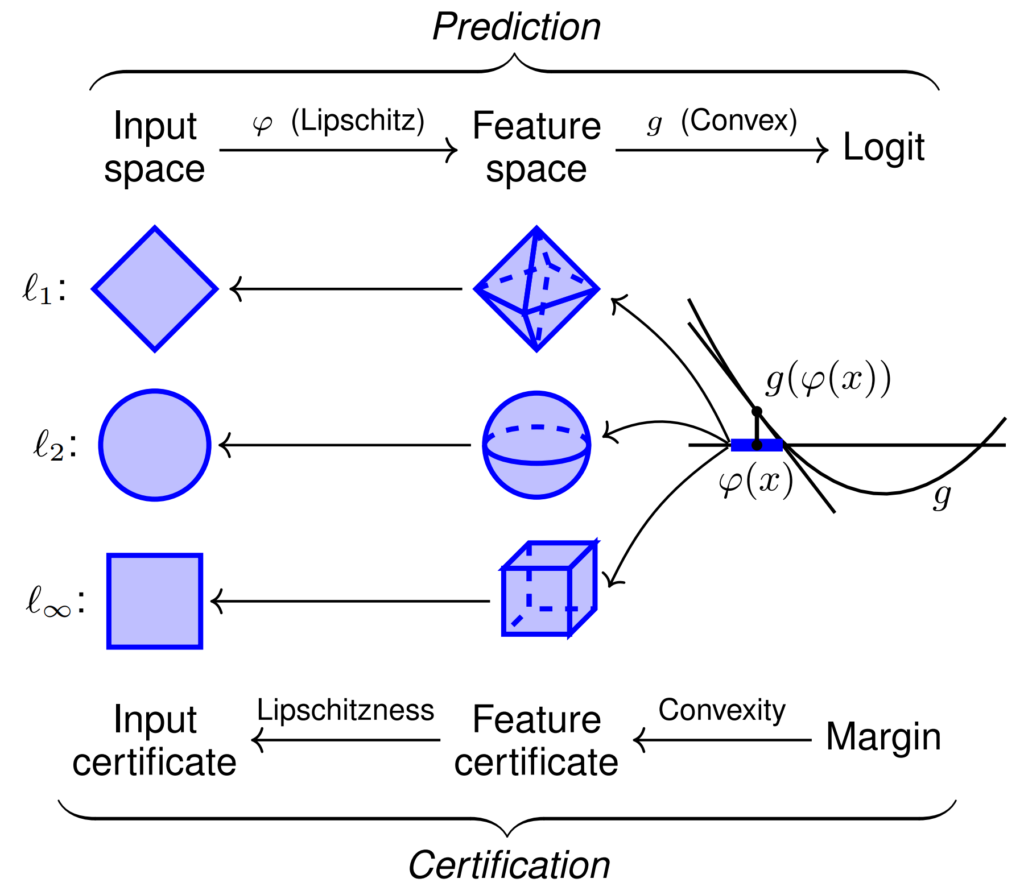
Figure 1. Example of feature-convex classifiers and their validation for sensitive-class input. This architecture constructs a Lipschitz-continuous feature map $varphi$ with a learned convex function $g$ . Since $g$ is convex, it is globally less than its tangent plane at $varphi(x)$ , yielding certified normal balls in the characteristic space. The Lipschutzness of $varphi$ then obtains an appropriate scale certificate in the original input space.
Despite their widespread use, deep learning classifiers are severely vulnerable. Counterexamples: Small, humanly imperceptible image glitches that fool machine learning models into misclassifying modified input. This vulnerability severely compromises the reliability of security-critical processes involving machine learning. Many experimental defenses have been proposed against hostile perturbations—often only later defeated by stronger attack strategies. So we focus Certified robust classifierswhich provide a mathematical guarantee that their predictions will be consistent for the $ell_p$ -norm ball around an input.
Traditional certification robustness methods have many drawbacks, including nondeterminism, slow execution, poor scaling, and certification against the one-attack-only principle. We argue that these problems can be addressed by refining the deterministic robustness problem to be more compatible with practical adversarial settings.
The Problem of Asymmetric Certified Robustness
Current verifiably strong classifiers generate certificates for inputs belonging to any class. For many real-world adversarial applications, this is unnecessarily broad. Consider the ideal case of someone composing a phishing scam email while trying to avoid spam filters. This adversary will always try to fool the spam filter into thinking its spam email is benign—not the other way around. in other words, The attacker is purely trying to induce false negatives from the classifier.. Similar settings include malware detection, fake news flagging, social media bot detection, medical insurance claims filtering, financial fraud detection, phishing website detection, and more.
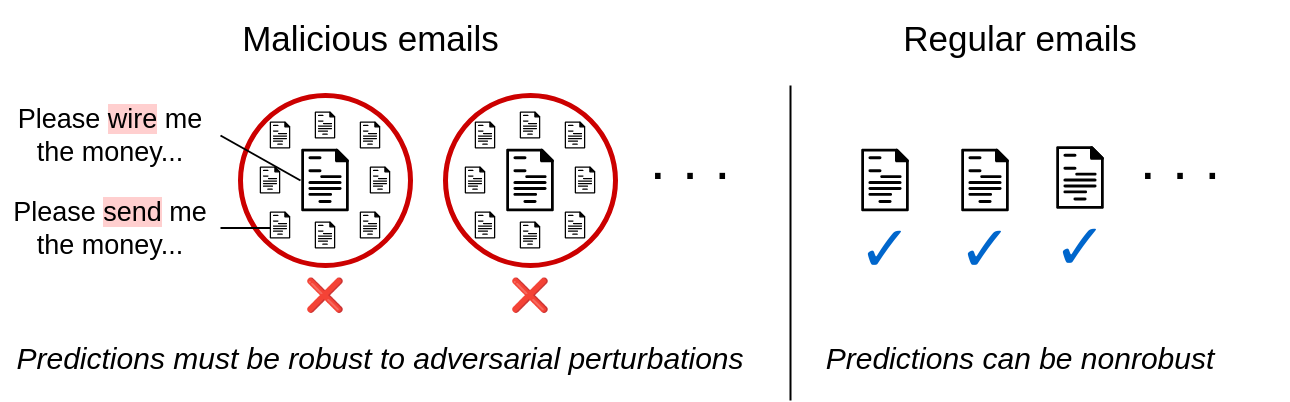
Figure 2. Asymmetric robustness in email filtering In practical adversarial settings, only one class of authentication is often required.
All these applications include a binary hierarchical configuration. Sensitive classes which an adversary is trying to avoid (eg, the “spam email” class). This encourages the problem Asymmetric certified strengthThe goal is to provide provably robust predictions for sensitive class inputs while maintaining a high clean accuracy for all other inputs. We provide a more formal problem statement in the main text.
Feature convex classifiers
We suggest. Feature Convex Neural Networks To solve the problem of asymmetric strengthening. This architecture maps a simple Lipschitz-continuous feature to ${varphi: mathbb{R}^d to mathbb{R}^q}$ with a learned Input-Convex Neural Network (ICNN). is ${g: mathbb {R}^q to mathbb{R}}$ (Figure 1). ICNNs implement convexity from input to output logit by composing ReLU nonlinearities with non-negative weight matrices. Since a binary ICNN decision region consists of a convex set and its complement, we add a predefined feature map $varphi$ to allow for non-convex decision regions.
Feature-convex classifiers enable fast computation of sensitive-class certified radii for all $ell_p$ -criteria. Using the fact that convex functions are globally less approximations than any tangent plane, we can obtain a constant radius in the intermediate feature space. This radius is then propagated to the input space by Lipschutzens. The asymmetric order is important here, since this architecture only produces certificates for the positive logit class $g(varphi(x)) > 0$ .
The resulting $ell_p$ -norm certified radius formula is particularly elegant:
[r_p(x) = frac{ color{blue}{g(varphi(x))} } { mathrm{Lip}_p(varphi) color{red}{| nabla g(varphi(x)) | _{p,*}}}.]
The non-constant terms can be easily interpreted: on a scale proportional to the radius Rating confidence And vice versa Classification sensitivity. We evaluate these certificates in a range of datasets, obtaining competitive $ell_1$ certificates and comparable $ell_2$ and $ell_{infty}$ certificates—although other methods generally meet a certain standard. are tailored and require orders of magnitude more runtime. .
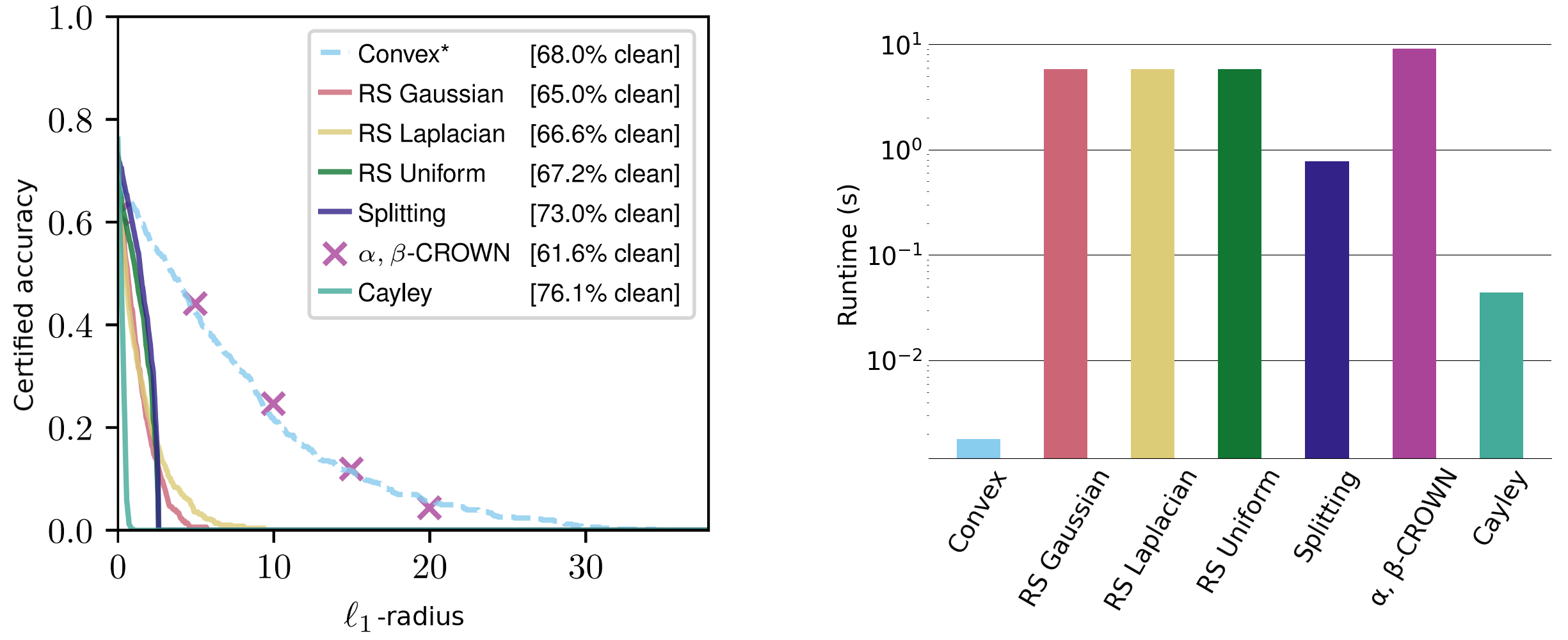
Figure 3. Certified radii of the sensitive class on the CIFAR-10 cats versus dogs dataset for $ell_1$-normality. Runtimes on the right are averaged over $ell_1$ , $ell_2$ , and $ell_{infty}$ -radii (note the log scaling).
Our certificates hold for any $ell_p$ -norm and are closed-form and deterministic, requiring only one forward and one backpass per input. They are computable on the order of milliseconds and scale well with network size. By comparison, current state-of-the-art methods such as random smoothing and interval-bound propagation typically take several seconds to verify even small networks. Random smoothing methods are also inherently nondeterministic, with certificates that hold only with high probability.
Theoretical promise
Although preliminary results are promising, our theoretical work shows that there is significant untapped potential in ICNNs, even without a feature map. Despite limiting binary ICNNs to learning convex decision regions, we prove that there is an ICNN that achieves training accuracy on the CIFAR-10 cats-vs-dogs dataset.
Reality There is an input convex classifier that achieves the best training accuracy for the CIFAR-10 cats-versus-dogs dataset.
However, our architecture achieves only $73.4%$ training accuracy without a feature map. Although training performance does not imply generalization to the test set, this result suggests that ICNNs are at least theoretically capable of achieving the modern machine learning paradigm of overfitting the training dataset. We thus generate the following open problem for the field.
Open problem. Learn an input convex classifier that achieves better training accuracy for a dataset of dogs than CIFAR-10 cats.
Result
We hope that the asymmetric robustness framework will inspire new architectures that are verifiable in this more focused setting. Our feature convex classifier is a similar architecture and provides fast, deterministic guaranteed redis for any $ell_p$-normal. We also present the open problem of overfitting the CIFAR-10 cats versus dogs training dataset with ICNN, which we show is theoretically feasible.
This post is based on the following paper:
Asymmetric confirmation robustness by feature-convex neural networks
Samuel Frommer,
Brandon G. Anderson,
Julian Peet,
Soumya Sojodi,
37th Conference on Neural Information Processing Systems (NeurIPS 2023).
More details are available at arXiv And GitHub. If our paper influences your work, please consider citing it with:
@inproceedings{
pfrommer2023asymmetric,
title={Asymmetric Certified Robustness via Feature-Convex Neural Networks},
author={Samuel Pfrommer and Brendon G. Anderson and Julien Piet and Somayeh Sojoudi},
booktitle={Thirty-seventh Conference on Neural Information Processing Systems},
year={2023}
}